基础入门
什么是数据结构?
数据结构是计算机存储、组织数据的方式。简而言之,数据结构是相互之间存在一种或多种特定关系的数据元素的集合,即带“结构”的数据元素的集合,“结构”就是指数据元素之间存在的关系,分为逻辑结构和存储结构。
逻辑结构
所谓逻辑结构,指的是数据及数据间的邻接关系。说白了它描述数据间是以什么方式排列的,而与他们在计算机中的存储位置无关。常见的逻辑结构有如下几种:
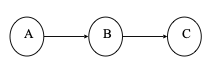
1、线性结构
结构中的元素存在1对1的关系。如下图A、B、C,每个结点最多只有一个直接前驱和一个直接后继,即从前到后顺序排列元素。
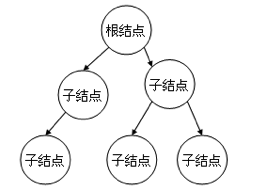
2、树形结构
结构中的元素存在1对多的关系。如下图所示,一个结点可以有多个子结点,但每个结点只能有一个父结点,元素按照上下级的顺序排列。
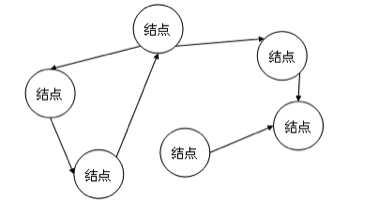
3、图状结构
结构中的元素存在多对多的关系。如下图所示,元素之间没有上下级的关系,只有邻接关系。
4、集合
结构中数据元素除了同属一个集合外,别无任何关系。
存储结构
逻辑结构只是在现实世界中对数据的排列方式进行描述,我们需要在计算机中实现它。
数据的逻辑结构在计算机内的表示称为数据的存储结构,其对逻辑结构的表示有两方面:
1、对逻辑结构中数据元素的表示(通过2进制表示)。
2、对逻辑结构中数据间的邻接关系的表示。
在计算机中数据间的邻接关系有4种:顺序存储、链式存储、索引存储、散列存储:
一般使用顺序存储或者链式存储来表示线性结构。
一般使用链式存储来表示树形结构和图状结构。
一般使用散列存储来表示哈希表。
算法分析
算法(Algorithm) :即完成某件事所用的步骤、方法。
算法的五大特性
第一,有穷性: 算法能在合理的时间内执行完毕,执行1000年的算法不具备有穷性。
第二,可行性: 算法中的所有步骤必须是计算机能做到的,除数为0就不具备可行性。
第三,确定性: 算法中的每一步都必须清楚,不能有歧义。
第四、五,输入/输出性: 算法可以没有输入,但是必须要有输出。
计算机中为什么除数不能为0?
0在数学中代表着无穷小,无穷小的倒数就是无穷大,任何数除以0得到的结果都是无穷大,而无穷大意味着计算机为了表示这个无穷大的数,内存会被填满,因此不允许除数0。
算法设计的要求
设计一个算法要求: 正确性、健壮性、可读性、效率。其中:
健壮性:也称为鲁棒性,当输入的数据非法时,算法也能应对,即算法是否能经受住各种数据的考验。
效率:指的是算法的执行时间与存储量。
说白了一个算法好与坏的评价标准是:正确,可读,健壮,效率高,空间省!
算法效率的度量
常用的度量算法效率的指标是:
时间复杂度:在最坏情况下,估计算法执行时间的一个上界,采用大O(字母O)记法。
空间复杂度:用来度量算法所需的存储空间,就是算法产生的数据所占据的空间。
时间复杂度,就是程序中基本操作语句执行的次数。如:1
2for(int i=0;i<100;i++)
sum+=i;
其中sum+=i执行了100次,而for(int i=0;i<100;i++)执行了101次,因此整个程序的时间复杂度为101或者说为n,因为100是一个常数,程序的执行次数会随着这个常数的变化而变化,因此,一般就称其复杂度为n,即线性增长。
在分析时间复杂度时,应该以程序或算法中执行次数最多的语句为准,通常情况下是最内层循环的时间复杂多,最内层语句的执行次数计算出来后,取最高的次幂(其他低次幂直接忽略掉),然后去掉该项中的常数因子即可。
本节参考阅读:
线性结构
线性表
线性表 (Linear_List) 简称表,由具有相同类型的有限多个数据元素组成的一个有序序列。
表中数据元素的个数n称为表的长度,长度为0的是空表,在非空线性表中,只有一个首元素和一个尾元素,中间元素有且仅有一个直接前驱和直接后继。
线性表按照元素的排列顺序分为:
有序表:如果线性表中的元素的值按递增(减)顺序排列,则此表称为有序表。
无序表:否则称为无序表。
线性表按照表的存储结构分为:
静态存储:表中元素存放在连续的空间中,使用顺序式存储方式,一般使用数组表示。
动态存储:表中元素存放在不连续的空间中,使用链式存储方式,一般需要自己构建链表。
顺序表
静态存储在计算机内的表示形式就是:顺序表。
特点:在内存中开辟连续的存储空间,顺序存储每一个数据元素,两个元素紧挨着存储。
优点:顺序表一般使用数组实现,可以使用数组的下标,对元素进行高速的存取。
缺点:插入和删除的时候,需要移动元素,尤其是在数组中具有很多元素的情况下,在数组的前部进行数据的插入和删除操作。
范例1:顺序表的常见操作。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
int Count = 0; //定义一个全局变量,用来代表数组内当前元素的个数
int insert(int array[],int element){ //本函数用于向数组中插入元素 。
if(Count == MAX){ //如果数组已经满了,则不允许插入新数据。
return -1;
}else{
array[Count++] = element; //否则,就将新数据插入数组,并且更新Count。
}
return 1;
}
void print(int array[]){ //本函数用于将所有元素输出 。
int i ;
for(i=0;i<Count;i++){ //遍历数组,从0开始,一直到最后一个元素结束。
printf("%d ",array[i]);
}
putchar('\n');
}
int remove(int array[],int element){ //本函数用于删除指定的元素 。
int index,i;
index = search(array,element); //先查找元素是否存在 。
if(index != -1){ //如果元素存在,则开始删除操作 。
for(i=index+1;i<Count;i++){ //将待删元素之后的所有元素都前移一个位置 。
array[i-1] = array[i];
}
Count-- ; //删除成功后,别忘了更新Count 。
return 1; //然后函数返回1 。
}else{ //如果元素不存在,则返回-1 。
return -1;
}
}
int search(int array[],int element){ //本函数用于 查找指定元素在数组中的下标。
if(Count == 0){ //如果数组为空,则直接返回-1。
return -1;
}else{ //如果数组不为空,则开始进行查找操作。
int i ;
for(i=0;i<Count;i++){ //遍历数组,从0开始依次匹配元素。
if(array[i] == element){ //如果找到了,则返回这个元素的下标。
return i;
}
}
return -1; //如果最终没有找到,则返回 -1 。
}
}
语句解释:
- 上面列出了最基础的三个操作:增、删、查。
链表
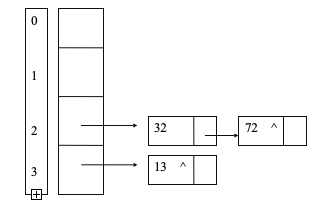
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针实现的,而所谓的动态存储落实到计算机中,就是通过链表来实现的。
简单的来说,链表其实就像是火车一样,火车有一个火车头,其后跟着N节车厢,各节车厢尾部都有一个“挂钩”,用于与其他车厢首尾相连,而最后一个车厢尾部是没有挂钩的,或者有挂钩,但是并不去使用它。
链表也是如此,每个元素都是链表的一个节点,每个节点内部也都有一个指针,指向下一个节点。同时也有链表头的概念,一个链表全靠表头作为起点,没有表头,根本就没法找到这个链表中的其他元素。
关于链表还需要知道的是:
特点:链表中的结点分散在内存中的各个角落,相邻的结点间通过指针联系。
优点:链表中的结点,只有在需要的时候才去建立,不必事先开辟过多空间,且删除和增加结点时,不需要移动元素。
缺点:链表不可以高速存取,结点的存储密度低。
范例1:链表的常见操作。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
struct Node{ // 定义一个结点结构体。
int sid; //数据域。
struct Node *next; //指针域。
};
//为struct Node类型起一个别名Student,以方便后面建立变量。
typedef struct Node Student;
//建立一个链表的头结点,以此为链表的表头。
Student *head = NULL;
void insert(Student *e){ //本函数用来向链表的表尾增加一个结点。
if(head == NULL){ //如果链表的表头为空。
head = e; // 则将这个结点作为此链表的第一个元素 插入到表头。
}else{ //如果表头结点不为空,说明链表中已存在结点,则继续向下执行。
Student *p = head; //将表头结点的地址取出,开始遍历链表。
while(p->next != NULL){ //一直遍历到链表的最后一个结点为止。
p = p->next;
}
p->next = e; //使最后一个结点的next指针指向新结点。
}
}
void print(){ //本函数用来遍历链表。
Student *p = head; //将表头结点的地址取出,开始遍历链表。
while(p != NULL){ //如果p不是最后一个结点。
printf("%d ",p->sid); //则将p的值输出。
p = p->next; //p指向下一个结点。
}
putchar('\n'); //遍历完所有结点后,换行。
}
Student* search(int keyword){ //本函数用来查找链表中的元素。
if(head == NULL){ //如果链表为空,则直接返回NULL。
return NULL;
}else{ //如果链表不为空,则开始查找。
Student *p = head; //开始遍历链表。
while(p!=NULL){ //如果p正在指向一个具体的结点。
if(p->sid == keyword){ //判断当前结点是否和指定关键字相等。
return p; //如果相等的话,则返回p结点。
}
p = p->next; //否则继续遍历下去。
}
return NULL; //如果到最后仍然没有找到,则返回NULL。
}
}
int remove(int keyword){ //本函数用来删除链表中的元素。
if(head == NULL){ //如果链表为空,则直接返回-1。
return -1;
}else{ //如果链表不为空,则开始进行匹配。
if(head->sid == keyword){ //如果头结点是待删结点。
head = head->next; //则直接让头结点指向下一结点。
return 1; //删除成功,返回1。
}else{ //如果头结点不是待删结点。
Student *p1,*p2; //准备遍历链表。
p1 = p2 = head; // p2用来代表当前结点,p1用来保存p2前面的那一个结点。
while(p2!=NULL && p2->sid != keyword){ //如果p2不是待删结点。
p1 = p2; //使p1指向p2。
p2 = p2->next; //p2指向下一个结点。
}
if(p2 != NULL){ //如果p2是待删结点。
p1->next = p2->next; //让p2前面的结点p1的next指针指向p2的next。
return 1; //删除成功返回1。
}else{
return -1; //在当前链表中,没找到待删元素,返回-1。
}
}
}
}
语句解释:
- 上面列出了最基础的三个操作:增、删、查。
- 链表中最后一个结点的next指针为NULL。
上面介绍的就是最简单的单链表,除此之外,还有如下三种链表:
双(向)链表:结点中包含有2个指针,分别指向结点的直接前继和直接后继。
双端链表:是单链表的变形,具有表头和表尾2个指针,因为在实际应用中经常要在表头和表尾进行插入删除等操作。后面讨论链队的时候,会仔细讲解。
循环表:循环表的最后一个结点的next指针不为null,而是指向了表的第一个结点,只要知道某一结点的地址就可以找到该表的所有结点。
线性表小结
顺序表:元素顺序存放在一片连续的存储空间中的表。
优点:可以高速存取,结点的存储密度高。
缺点:需要开辟连续的存储空间,长度固定。
使用场合:适合于处理少量数据时使用。
链表:元素随机分布在内存的各个地方,各元素之间通过指针来连接。
优点:不需要开辟连续的存储空间,链表长度可变。
缺点:结点的存储密度低、不能随机存取。
使用场合:链表的适合于处理中少量的数据时使用。
上面说在链表中结点的存储密度低,原因如下:
假设一个结点占20字节,如果用顺序表存储数据,则这20字节可以全用来存储数据。
如果使用链表,则至少要分出一些字节,作为指针域,存储下一个结点的信息。
因此,所谓的存储密度就是在说,结点中存储空间利用的是否充分。
栈
栈(Stack) :只允许在表的一端进行插入和删除的线性表,允许插入和删除的一端称为栈顶(top), 另一端称为栈底(bottom)。
特点: 后进先出、后来居上。
分类: 顺序栈和链栈。
常见的操作:压栈、弹栈、判断栈空、返回栈顶、栈内元素个数。
范例1:顺序栈。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int Count = 0; //记录当前栈中的元素个数。
int push(int array[],int element){ //本函数用来完成压栈操作。
if(Count == MAX){ //如果栈满了,则不允许压栈。
return -1; //返回-1 。
}else{ //如果栈未满,则开始压栈。
array[Count++] = element; //将元素放到数组的最后一个位置。
return 1; //压栈成功,返回1。
}
}
void print(int array[]){ //本函数用来遍历栈中的元素。
int i ;
puts("栈-----------------------顶");
for(i=Count-1;i>=0;i--){//从最后一个元素开始输出,因为数组的最后一个元素代表栈顶。
printf("\t %d\n",array[i]);
}
puts("栈-----------------------底\n");
}
int size(){ //本函数用来获得栈中元素的个数。
return Count;
}
int isEmpty(){ //本函数用来判断栈是否为空。
return Count == 0 ;
}
int peek(int array[]){ //本函数用来返回栈中的当前栈顶元素。
if(Count == 0){ //如果栈空,则返回-1。
return -1;
}else{
return array[Count-1]; //如果栈没空,则返回栈顶元素。
}
}
int pop(int array[]){ //本函数用来弹出当前栈顶元素。
if(Count == 0){ //如果栈空,则返回-1。
return -1;
}else{
return array[--Count]; //如果栈没空,则弹出栈顶元素。
}
}
main(){
int i ,array[MAX]; //定义一个数组,用来代表顺序栈。
for(i=0;i<MAX;i++){ //向栈中压入MAX个元素。
push(array,i); //通过调用push()函数,来向栈中压入数据。
print(array); //每压入一个数据,都遍历一遍栈中的元素。
}
}
语句解释:
- 上面列出了最基础的三个操作:增、删、查。
- 压栈的算法和顺序表增加元素的算法是一样的,数组的最后一个元素,代表顺序栈的栈顶,第一个元素代表顺序栈的栈底。
- 本范例只是作为一个范例,若栈内有一个数据元素本身的值就是-1 ,则本范例没有对产生的歧义进行处理。
范例2:链栈。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
struct Node{ //定义一个结点类型。
char info[20]; //结点的数据域。
struct Node *next; //指向下一个结点的指针。
};
typedef struct Node Student; //给这个结点类型 起一个别名Student。
Student *head=NULL; //定义一个栈顶指针。
void push(Student *element){ //本函数用来将一个结点压入栈顶。
if(head == NULL){ //如果栈顶为空,则将元素压入栈顶。
head = element;
}else{ //如果栈顶不为空。
element->next = head; //让新元素的next指向当前栈顶。。
head = element; //然后使head指针指向新元素。
}
}
void print(){ //本函数用来遍历栈中的元素。
Student *p; //定义一个用来遍历的指针。
p = head; //最初,使指针p指向栈顶元素。
while(p != NULL){ //如果p当前所指向的位置,不是栈底。
printf("\t\t%s\n",p->info); //输出当前位置的数据。
p = p->next; //p指向栈中的下一个元素。
}
putchar('\n'); //换行。
}
int size(){ //本函数用来获取栈中元素的个数。
Student *p; //定义一个用于遍历栈的指针。
int i = 0; //用来计算栈中元素的个数,从0开始累计。
p = head; //p从栈顶元素开始遍历。
while(p != NULL){ //如果p当前所指向的位置,不是栈底。
p = p->next; //p指向栈中的下一个元素。
i++; //变量增加1。
}
return i; //返回最终的结果。
}
char * peek(){ //本函数用来获取栈顶元素中info成员的信息。
if(head == NULL){ //如果栈空。
return "null"; //则返回一个字符串常量。
}else{ //如果栈非空。
return head->info ; //则返回栈顶元素中的info成员的信息。
}
}
int pop(){ //本函数用来弹出栈顶元素。
if(head == NULL){ //如果栈空 则返回-1。
return -1;
}else{ //如果栈非空。
head = head->next; //栈顶指针下移一个位置。
return 1; //返回1。
}
}
语句解释:
- 上面列出了最基础的三个操作:增、删、查。
- 压栈的算法和顺序表增加元素的算法是一样的,数组的最后一个元素,代表顺序栈的栈顶,第一个元素代表顺序栈的栈底。
- 本范例只是作为一个范例,若栈内有一个数据元素本身的值就是-1 ,则本范例没有对产生的歧义进行处理。
接下来介绍一些算法,来展示一下栈的实际应用。
递归
程序调用自身的编程技巧称为递归( recursion)。
接下来,我们通过计算“N!”来介绍递归的写法,其中“N!”表示N的阶乘,即任何大于等于1的自然数n 阶乘表示方法:

范例1:阶乘。1
2
3
4
5
6
7public long fact(int num) {
if(num<=1) { //解决
return 1;
} else { //分解
return num*fact(num-1); //合并
}
}
语句解释:
- 递归一定要有一个结束的条件,否则程序就没有出口了,本范例中当num<=1时程序就不会继续向下递归了。
其实递归属于计算机科学中的一个名为“分治法”的算法。
字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
分治法是通常是通过函数递归来实现的,其在每一层递归上都有三个步骤:
分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题。
合并:将各个子问题的解合并为原问题的解。
方法/函数的递归,就是利用了栈的原理,后来居上,同时会从最上面开始解决问题。
范例2:汉诺塔算法(Hanoi)。
有A、B、C三座塔,其中在A塔上,从下到上地穿好了由大到小的64片金片。
任务规则:
1、将A塔上面的盘子,全部移动到C塔上。
2、一次只能移动一个盘子。
3、不论将盘子移动到哪座塔,都需要保证小盘子在大盘子上面,始终保持“上小下大”的顺序。
显然,要完成任务需要三步:
第一步,要想将A塔上的第64个盘子到C塔,需要将前63个盘子移到B塔上。
第二步,将第64个盘子移到C塔。
第三步,将移走的前63个盘子从B塔中移回到C塔的第64个盘子的上面。
1 | public class Hanio { |
范例3:螺旋数。
从键盘输入一个整数(1~20),则以该数字为矩阵的大小,把1,2,3 … n(n+1)/2 的数字按照顺时针螺旋的形式填入其中。如:
输入数字3,则程序输出:
1 2 3
6 4
5
输入数字4,则程序输出:
1 2 3 4
9 10 5
8 6
7
1 | public class HelixNumber { |
迷宫
迷宫首先得有一张地图,一般来说都使用一个二维数组来表示地图,二维数组a[i][j]上的值为1代表墙,为0则代表路,如下图所示:
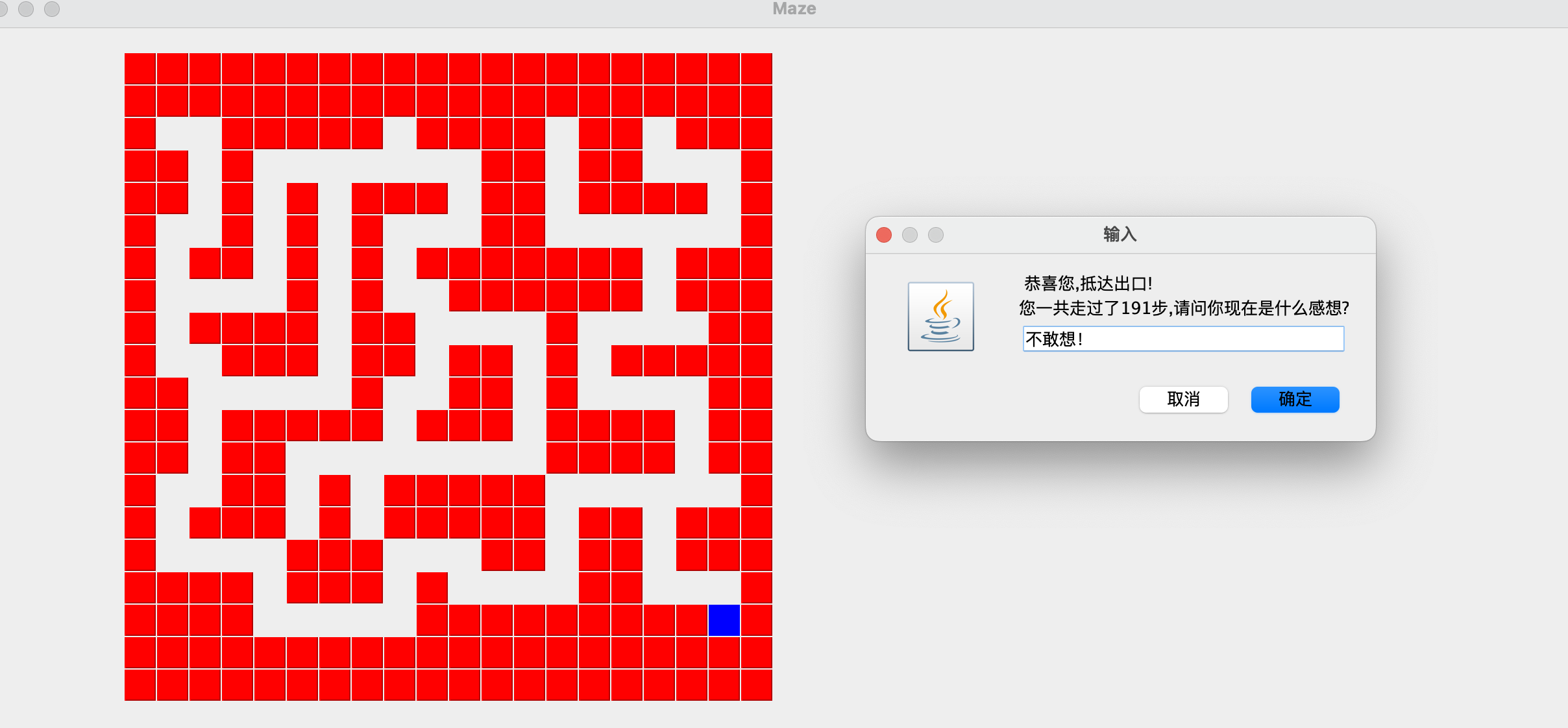
有了地图之后呢,很显然咱们得规定一个起点和终点,并且将游戏者放到起点上去。
从起点开始,按东、南、西、北的顺序开始走,将走过的所有路都置为1(同时压栈),以防止重复走,如果走到了死路,则回到上一步(弹栈),一直到走到终点为止。
下面是迷宫程序的完整JAVA源代码,一共三个类,可以直接运行:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221/**
* 功能:
* 1. 本类是迷宫程序的入口类,提供了main方法。
* 2. 本类同时用来构建迷宫程序的主界面。
* 3. 用户鼠标左键点击窗口中的任意位置即可开始游戏。
*/
public class MazeFrame extends JFrame {
public static final String FRAME_TITLE = "Maze";
public MazeFrame(){
// 设置窗口的标题、在屏幕中的初始位置、窗口的宽高。
super(FRAME_TITLE);
setBounds(0, 0, 800, 600);
// 设置用户点击窗口右上角的关闭按钮的动作,此处为摧毁当前JFrame窗口。
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
// 将界面设置到当前JFrame中。
MazePanel panel = new MazePanel();
add(panel);
}
public static void main(String[] argss){
MazeFrame mazeFrame = new MazeFrame();
// 将主窗口置为可见状态。
mazeFrame.setVisible(true);
}
}
/**
* 功能:本类用来描述一个栈。
*/
public class MazeStack<T> {
private ArrayList<T> array; // 使用一个List对象来保存栈中的元素。
private int now_count; // 记录当前栈中所具有的元素的个数。
public MazeStack() {
now_count = 0;
array = new ArrayList<T>();
}
public Point pop() {
if (now_count == 0) {
throw new EmptyStackException();
} else {
now_count--;
return (Point) array.remove(now_count);
}
}
public void push(T point) {
array.add(point);
now_count++;
}
public Point peek() {
if (now_count == 0)
throw new EmptyStackException();
else
return (Point) array.get(now_count - 1);
}
public boolean isEmpty() {
return now_count == 0;
}
public int getCount() {
return now_count;
}
}
public class MazePanel extends JPanel implements ActionListener {
// 游戏者的当前位置,Point是系统内置的类,其中包含了x和y两个坐标值。
private Point now_point;
private Point start_point; // 游戏的起点位置。
private Point final_point; // 游戏的终点位置。
// 记录游戏者最终找到的一条正确的路线中的所有位置。
private MazeStack<Point> finalPath;
// 记录游戏者所有走过的路线中的所有位置。
private ArrayList<Point> allPath;
private int mapCopy[][]; // 地图副本。
// 游戏者的当前所走的步数,其值最初时为0。
// 此变量在程序模拟游戏者找路的过程时使用。
private int stepCount;
private boolean isStarting = false; // 标识程序当前是否处于 “开始游戏” 状态。
private Timer time;
private Rectangle2D player; // 使用一个长方形来代表游戏者。
public static final int PASS_BY = 2;// 标识当前位置已经被走过。
// 迷宫地图。0代表可走,1代表墙,2代表已走过。
private int map[][] =
{ { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
{ 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1 },
{ 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1 },
{ 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1 },
{ 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1 },
{ 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1 },
{ 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1 },
{ 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1 },
{ 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1 },
{ 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1 },
{ 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1 },
{ 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1 },
{ 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1 },
{ 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1 },
{ 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1 },
{ 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1 },
{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 } };
public MazePanel() {
// 初始化地图副本。
mapCopy = new int[map.length][map.length];
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[i].length; j++)
mapCopy[i][j] = map[i][j];
}
// 将游戏者的初始位置置为地图上的 (2,1) 并将该位置压入栈中 。
start_point = now_point = new Point(2, 1);
finalPath = new MazeStack<Point>();
finalPath.push(now_point);
// 设置游戏的终点位置。
final_point = new Point(17, 18);
// 为当前JPanel添加鼠标事件监听器,以便用户点击窗口任意位置后,开始游戏。
addMouseListener(new MouseAdapter() {
public void mouseClicked(MouseEvent mouseevent) {
// 若还没有开始游戏。
if (!isStarting) {
isStarting = true;
// 游戏者会从(2,1)点出发,探索整个迷宫。
walk(start_point.x, start_point.y);
// 执行到此处,表示已经探索完迷宫并已经找到出口。
// 下面的代码用来播放玩家行走路线,每一步间隔80毫秒。
time = new Timer(80, MazePanel.this);
time.start();
}
}
});
allPath = new ArrayList<Point>();
}
/**
* 游戏者开始行走。
*/
public void walk(int i, int j) {
// 记录当前位置。
allPath.add(new Point(i, j));
// 若当前位置是终点。
if (i == final_point.x && j == final_point.y) {
System.out.println("恭喜您,程序找到出口了! 正确的行走步骤为:");
int k;
for (k = 0; !finalPath.isEmpty(); k++) {
Point temp = finalPath.pop();
System.out.println("( " + temp.x + " , " + temp.y + " )");
}
System.out.println("系统:经过辛苦的计算,成功抵达出口,一共需要走 "
+ k + " 步。");
} else {
map[i][j] = PASS_BY; // 标识当前位置已经被走过。
if (map[i][j + 1] == 0) {
// 若当前位置的东部(上北下南左西右东)仍然可以行走,则向东走。
finalPath.push(new Point(i, j + 1));
walk(i, j + 1);
}
if (map[i + 1][j] == 0) {
// 若当前位置的南部仍然可以行走,则向南走。
finalPath.push(new Point(i + 1, j));
walk(i + 1, j);
}
if (map[i][j - 1] == 0) {
// 若当前位置的西部仍然可以行走,则向西走。
finalPath.push(new Point(i, j - 1));
walk(i, j - 1);
}
if (map[i - 1][j] == 0) {
// 若当前位置的北部仍然可以行走,则向北走。
finalPath.push(new Point(i - 1, j));
walk(i - 1, j);
}
// 若当前位置旁边的四个方向都走不通(已走过或是死路),则返回上一步。
if (!finalPath.isEmpty()) {
this.allPath.add(finalPath.pop());
}
}
}
/**
* 功能:通过定时器来模拟游戏者的行走过程。
*/
public void actionPerformed(ActionEvent actionevent) {
if (now_point.x != final_point.x || now_point.y != final_point.y) {
now_point.x = ((Point) allPath.get(stepCount)).x;
now_point.y = ((Point) allPath.get(stepCount)).y;
stepCount++;
repaint(); // 重绘界面。
System.out.println("( " + now_point.x + " , " + now_point.y + " )");
} else {
String msg = JOptionPane.showInputDialog(null,
" 恭喜您,抵达出口!\n您一共走过了" + stepCount
+ "步,请问你现在是什么感想?");
JOptionPane.showMessageDialog(null, msg + " ? 哈哈,那恭喜您了");
// 停止定时器。
time.stop();
}
}
public void paint(Graphics g) {
super.paint(g);
Graphics2D graphics2d = (Graphics2D) g;
for (int i = 0; i < mapCopy.length; i++) {
for (int j = 0; j < mapCopy[i].length; j++) {
player = new java.awt.geom.Rectangle2D.Double(i * 25 + 110,
j * 25 + 20, 24D, 24D);
if (mapCopy[j][i] == 0) {
if (j == now_point.x && i == now_point.y) {
graphics2d.setPaint(Color.blue);
graphics2d.fill(player);
}
} else {
graphics2d.setPaint(Color.red);
graphics2d.fill3DRect(i * 25 + 110, j * 25 + 20,
24, 24, true);
}
}
}
}
}
表达式求值
一个表达式由操作数、操作符和分界符三部分组成:
比如表达式“(3+4)/2”
其中3、4、2是操作数,+、/是操作符,括号是分界符
拿上面的表达式来说,表达式的结果我们看一眼就知道,但是计算机不能像咱们这样做,因为它不会,为了让计算机能正确算出结果,我们需要准备2个栈,一个是符号栈(用来存放操作符),另一个是数字栈(用来存放操作数)。
计算机会从左到右顺序扫描表达式,并进行如下判断:
若是操作数,则直接压入数字栈。
若是操作符,则进一步判断:
若当前符号栈为空,则直接将该运算符压入符号栈。
若当前符号栈栈顶符号是左括号‘(’则也直接将该运算符压入符号栈。
若当前符号栈栈顶符号的优先级<该运算符,还是直接将该运算符压栈。
若当前符号栈栈顶符号的优先级>=该运算符,则将栈顶运算符(OP)取出来,接着从数字栈中取2个数b、a,将a(OP)b的结果压入数字栈中。
若当前符号是右括号‘)’,则不将它压入栈,而是不断从2个栈中,弹出1个符号和2个操作数,然后将运算结果压入数字栈,直到遇到左括号‘(’。
然后,继续向表达式的后面扫描,直到表达式结束。
下面是表达式求值程序的完整JAVA源代码,一共三个类,可以直接运行:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156// 链栈
public class LinkedStack<T> {
private Node<T> head;
public boolean push(T data) {
if (data == null)
throw new IllegalArgumentException("参数为null");
Node<T> curr = new Node<T>(data, head);
head = curr;
return true;
}
public T pop() {
if (head == null)
throw new NullPointerException();
T data = head.getData();
head = head.getNext();
return data;
}
public T peek() {
if (head == null)
throw new NullPointerException();
return head.getData();
}
public boolean isEmpty() {
return head == null;
}
}
// 链栈的节点类
public class Node<T> {
private T data;
private Node<T> next;
public Node(T data, Node<T> next) {
this.data = data;
this.next = next;
}
public T getData() {
return this.data;
}
public Node<T> getNext() {
return this.next;
}
public void setNext(Node<T> next) {
this.next = next;
}
}
// 表达式计算类
public class Expression {
private LinkedStack<Double> numStack; // 数字栈
private LinkedStack<Character> chStack; // 符号栈
public Expression() {
this.numStack = new LinkedStack<Double>();
this.chStack = new LinkedStack<Character>();
}
public double compulation(String expression) {
if (expression == null) {
throw new IllegalArgumentException("参数为null");
}
double value = Double.NaN;
try {
// 分解表达式 将结果放到符号栈和数字栈。
pushStack(expression);
// 不断的从符号栈弹出符号进行计算。
while (!chStack.isEmpty()) {
calc();
}
// 计算完后 栈顶元素就是表达式的结果。
value = numStack.pop();
} catch (Exception e) {
System.out.println("表达式不规范或者包含非法字符,停止计算!");
}
return value;
}
public void pushStack(String expression) {
StringBuffer str = new StringBuffer(expression);
char c = 0;
while (str.length() > 0) {
double num = 0;
// 尝试从字符串头部解析出一个数字
boolean mark = false;
while (str.length() > 0) {
c = str.charAt(0);
if (!(c >= '0' && c <= '9'))
break;
num = num * 10 + (c - 48);
str.deleteCharAt(0);
mark = true;
}
if (mark) {
numStack.push(num);
}
if (str.length() > 0) {
switch (c) {
case '(':
break;
case ')':
while (chStack.peek() != '(')
calc();
chStack.pop();
break;
case '*':
case '/':
case '%':
while (!chStack.isEmpty() && chStack.peek() != '('
&& (chStack.peek() == '*' || chStack.peek() == '/'
|| chStack.peek() == '%'))
calc();
break;
case '+':
case '-':
while (!chStack.isEmpty() && chStack.peek() != '(')
calc();
break;
}
if (c != ')')
chStack.push(c);
str.deleteCharAt(0);
}
}
}
private void calc() {
Double b = numStack.pop();
Double a = numStack.pop();
char op = chStack.pop();
switch (op) {
case '+':
numStack.push(a + b);
break;
case '-':
numStack.push(a - b);
break;
case '*':
numStack.push(a * b);
break;
case '/':
if (b != 0)
numStack.push(a / b);
break;
case '%':
numStack.push(a % b);
break;
}
}
public static void main(String[] args) {
Expression exp = new Expression();
System.out.print("输入表达式: ");
Scanner sc = new Scanner(System.in);
String expression = sc.next();
System.out.println(exp.compulation(expression));
}
}
语句解释:
- 输入“55-4*5+(4+1*100/(5-3))*3+(4+2)”,程序输出“203.0”。
关于表达式,还有以下两个小知识点,了解即可。
表达式的分类
中缀表达式:A+B
前缀表达式:+AB
后缀表达式:AB+
显而易见,操作符在前,则就叫前缀表达式,以此类推。
中缀式转后缀式
中缀式: a+b*(c-d)-e/f
后缀式: abcd-*+ef/-
转换过程:
1、在a+b*(c-d)-e/f中,最先计算(c-d),而c-d的后缀式就是cd-。
2、接着计算b*(cd-),因此就是bcd-*,就是把*放到式子的最后面。
3、然后计算a+(bcd-*),因此就是abcd-*+
4、接着计算e/f,因此就是ef/
5、最后计算(abcd-*+)-(ef/),因此结果就是abcd-*+ef/-。
队列
队列( Queue ):插入和删除操作必须分别在不同的两端进行的线性表。允许插入的一端称队尾,允许删除的一端称队首,
特点:先进先出。(FIFO,first in first out)
分类:顺序队 和 链队。
由于队列的插入和删除操作分别在表的两端进行,因此需要设置队头指针和队尾指针。
范例1:链队。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
struct Node{
int data; //结点中的数据域。
struct Node *next; //结点中的指针域。
};
typedef struct Node Node; //为结点结构体起一个别名,将struct Node改成 Node 。
typedef struct{ //定义一个队列结构体。
struct Node *front; //队列的队首指针。
struct Node *rear; //队列的队尾指针。
}Queue;
Queue* createQueue(){ //本函数用来建立一个队列。
Queue *que = (Queue *)malloc(sizeof(Queue *)); //从内存中开辟队列空间。
if(que == NULL){ //如果开辟失败,则返回NULL。
return NULL;
}
que->front = NULL; //如果开辟成功,则初始化队列的头指针。
que->rear = NULL; //初始化队列的尾指针。
return que; //返回这个队列。
}
Node* createNode(int i){ //本函数用来建立一个结点。
Node* temp = (Node *)malloc(sizeof(Node *)); //从内存中开辟结点空间。
if(temp == NULL){ //如果开辟失败,则返回NULL。
return NULL;
}
temp->data = i; //如果开辟成功,则初始化结点的数据域。
temp->next = NULL; //初始化结点的next指针。
return temp; //返回这个结点。
}
int isEmpty(Queue* que){ //本函数用来判断队列是否为空。
return que->front == NULL; //如果头指针为NULL 则就认为队列为空。
}
int insert(Queue* que,Node *element){ //本函数用来将元素入队。
if(element == NULL){ //如果元素为空,则不允许入队。
return 0;
}
if(isEmpty(que)){ //如果队列为空。
que->front = que->rear = element; // 头指针和尾指针同时指向新元素。
}else{ //如果队列不为空。
que->rear->next = element; // 则将新元素增加到当前队尾的后面。
que->rear = element; // 修改队尾指针。
}
return 1;
}
int peek(Queue* que,int *result){ //本函数用来返回队首元素。
if(isEmpty(que)){ //如果队列为空。
return 0; //则肯定无法返回队首元素。
}
*result = que->front->data; //如果队列非空,则将队首元素的data域的值赋值给result。
return 1; //返回成功。
}
void print(Queue* que){ //本函数用来遍历队列。
Node* p = que->front; //建立一个临时结点,从队首指针开始,向后遍历。
while(p != NULL){ //如果当前结点不为空。
printf("%d ",p->data); //输出当前结点的数据域。
p = p->next; //当前结点继续向后遍历。
}
putchar('\n'); //换行。
}
int remove(Queue* que){ //本函数用来将队列元素出队。
if(isEmpty(que)){ //如果队列为空 则返回0。
return 0;
}
que->front = que->front->next; //否则,使队列的队首元素指向下一个元素。
return 1; //返回成功标记。
}
语句解释:
- 上面列出了最基础的三个操作:增、删、查。
数组、矩阵
数组
数组(Array)本身也是一个数据结构,是线性表的推广。数组元素的个数是固定的,一旦数组定义完毕,其长度就不能再发生变化,且数组元素具有相同的数据类型。
使用n表示数组的维数:
当n=1时,称其为一维数组,一维数组是一个定长的线性表。
当n>1时,称其为多维数组,如二维数组。二维数组本身也是一个线性表,它的每一个元素都是一个线性表。
二维数组存储元素的方式:按行存储和按列存储。现在假设每个数据元素占用L个单元,m、n为数组的行和列(m,n>=1),且i表示行数j表示列数:
按行存储方式,地址计算公式:Loc(aij) = Loc(a11) + ((i-1)n+j-1)L
按列存储方式,地址计算公式:Loc(aij) = Loc(a11) +((j-1)m+i-1)L
矩阵
矩阵就是一个二维数组,它分为:
普通矩阵:元素分布无规律。
特殊矩阵:值相同的元素或零元素在矩阵中分布有一定的规律,其又可以分为对称矩阵和三角矩阵。
稀疏矩阵:零元素在矩阵中占比重非常大,且非0元素分布无规律。
其中特殊矩阵和稀疏矩阵可以被压缩存储。
之所以要对矩阵压缩,是因为矩阵是很多科学与工程计算问题中研究的数学对象,为了节省存储空间,才需要对他们进行压缩,而所谓的压缩存储是指:为多个值相同的元只分配一个存储空间,对零元不分配空间。
范例1:n*n二维数组倒置。1
2
3
4
5
6
7
8
9
10
11
12
13
14
main(){
int array[MAX][MAX]={1,2,3,4,5,6,7,8,9};
int i,j,temp;
for(i=0;i<MAX;i++){
for(j=i+1;j<MAX;j++){
temp = array[i][j];
array[i][j] = array[j][i];
array[j][i] = temp;
}
}
putchar('\n');
}
对称矩阵压缩
对称矩阵是指一个行列相等、以主对角线为对称轴,各元素对应相等(Aij == Aji)的矩阵。

所谓主对角线,就是指从矩阵左上角到右下角这一斜线方向上的n个元素所在的对角线。
上图中的红线就是主对角线。
对阵矩阵的存储空间为n²,我们只需要压缩其上三角(或下三角)+主对角线上的元素即可,压缩后有n*(n+1)/2个元素,可以存储在一个一维数组里。
范例1:下三角矩阵按行压缩。1
2
3
4
5
6
7
8
9
10
11int* zipArray(int array[][MAX]){ //本函数用来压缩一个对称矩阵。
int *temp = (int *)malloc(sizeof(int)*(MAX*(MAX+1)/2));
int i ,j,index;
for(i=0;i<MAX;i++){
for(j=0;j<=i;j++){
index = i*(i+1)/2+j; //计算aij在一维数组中的位置。
temp[index] = array[i][j]; //将aij存放到index指定的位置中去。
}
}
return temp; //返回压缩后的矩阵。
}
语句解释:
- 下三角按行压缩: index=i*(i+1)/2+j
- 上三角按列压缩: index=j*(j+1)/2+i
范例2:当然也可以这样。1
2
3
4
5
6
7
8
9
10
11int* zipArray(int array[][MAX]){
int *temp = (int *)malloc(sizeof(int)*(MAX*(MAX+1)/2));
int i ,j,index=0;
for(i=0;i<MAX;i++){
for(j=0;j<=i;j++){
// 直接这么写,就完事了。
temp[index++] = array[i][j];
}
}
return temp;
}
范例3:解压缩。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15int unzipArray(int *p,int i,int j){
int temp;
// 如果用户给出的坐标在下三角区。
if(j<=i){
// 使用下三角按行的压缩公式,将元素取出。
temp = p[i*(i+1)/2+j];
} else {
// 如果用户给出的坐标在上三角区。
// 在对称矩阵中,下三角按行压缩和上三角按列压缩,压缩出来的数组是一样的。
// 因此,如果用户输入的是上三角区的坐标,则应该用这个公式,来从一维数组中取数据。
// 使用上三角按列的压缩公式,将元素取出。
temp = p[j*(j+1)/2+i];
}
return temp;
}
语句解释:
- 所谓的解压缩,就是指给定一个数组p,以及i和j坐标,函数计算出该位置上元素的值。
三角矩阵压缩
三角矩阵是方形(n*n)矩阵的一种,因其“非C”元素的排列呈三角形状而得名,三角矩阵分上三角矩阵和下三角矩阵两种:
下三角矩阵:非C元素在矩阵的下三角区,反之则是上三角矩阵。
1 C C
2 3 C
4 5 6
其中C代表相同的一个常数,上面的矩阵可以换写成:
1 9 9
2 3 9
4 5 6
范例1:下三角按行压缩三角矩阵。1
2
3
4
5
6
7
8
9
10
11
12int* zipArray(int array[][MAX]){
int *temp = (int *)malloc(sizeof(int)*(MAX*(MAX+1)/2+1));
int i ,j,index;
for(i=0;i<MAX;i++){
for(j=0;j<=MAX;j++){
index = i*(i+1)/2+j;
temp[index] = array[i][j];
}
}
temp[MAX*(MAX+1)/2] = array[0][MAX-1];
return temp;
}
语句解释:
- 一个n*n的三角矩阵,压缩后一定为 n*(n+1)/2+1个元素。
- 上三角矩阵就压缩上三角,下三角矩阵就压缩下三角。
- 三角矩阵的压缩就是在对称矩阵的最后加一个元素而已。
稀疏矩阵
在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵。存储方法:
由于稀疏矩阵非0元素的分布没有什么规律可言,因此在存储非零元素值的同时,还必须存储它在矩阵中的位置(行号和列号)。
即每个结点至少要有:i、j、aij三个信息,我们称其为一个“三元组”。
元素的三元组,再加上一个特殊的三元组就组成一个稀疏矩阵的三元组表。
特殊的三元组:表示矩阵的行数、列数、以及非0元素的个数。
下面是一个3行4列的稀疏矩阵:
8 0 0 1
0 4 0 0
0 0 6 0
那么这个稀疏矩阵的三元组表:1
2
3
4M3*4 = {
{3,4,4},
{0,0,8}, {0,3,1}, {1,1,4}, {2,2,6},
}
矩阵乘积
首先,只有当矩阵A的列数与矩阵B的行数相等时A×B才有意义。
然后,一个矩阵a(m,n)乘以矩阵b(n,p),会得到矩阵c(m,p)。
那具体是如何乘的呢?假设有如下两个矩阵:
A:
1 2
3 4
5 6
B:
5 6 7
8 9 10
具体过程:
首先,用A的第一行依次乘以B的每一列。
C[0][0] = 1*5 + 2*8
C[0][1] = 1*6 + 2*9
C[0][2] = 1*7 + 2*10
然后,用A的第二行依次乘以B的每一列。
C[1][0] = 3*5 + 4*8
C[1][1] = 3*6 + 4*9
C[1][2] = 3*7 + 4*10
最后,用A的第三行依次乘以B的每一列。
C[2][0] = 5*5 + 6*8
C[2][1] = 5*6 + 6*9
C[2][2] = 5*7 + 6*10
矩阵乘法的两个重要性质:
矩阵乘法不满足交换律:假设A*B可以相乘,但是交换过来后B*A两个矩阵有可能根本不能相乘。
矩阵乘法满足结合律:假设有三个矩阵A、B、C,那么(AB)C和A(BC)的结果的第i行第j列上的数都等于所有A(ik)*B(kl)*C(lj)的和(枚举所有的k和l)。
范例1:矩阵乘积。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
main(){
int a[3][MAX]={1,2,3,4,5,6}; //定义一个3行2列的数组a。
int b[MAX][3]={5,6,7,8,9,10}; //定义一个2行3列的数组b。
int c[3][3]; //a和b的乘积是一个3行3列的数组。
int i,j,k;
for(i=0;i<3;i++){ // i 控制数组c的行数的变化。
for(j=0;j<3;j++){ // j 控制数组c的列数的变化。
int sum = 0; // 迭代变量。
for(k=0;k<MAX;k++){ // k控制数组a和b共同的部分。
sum +=a[i][k]*b[k][j]; // 开始计算。
}
c[i][j] = sum; // 将结果赋值给Cij 。
}
}
}
串
串:就是字符串,它是一种特殊的线性表,它的数据元素只能是字符,串可以为空,空串是任意串的子串。
基本操作: 合并(插入和连接)、删除子串、比较、倒置。
本节不会去介绍字符串的基本操作,而是会着重介绍字符串的“模式匹配”算法。
模式匹配
所谓模式匹配,就是找到子串(也称为模式串)在主串(也称为目标串)中出现的下标。
模式匹配有两种方法:
朴素模式匹配:朴素模式匹配没有KMP算法效率高,当目标串和模式串过长时,效率很低。
KMP模式匹配:KMP算法就是在目标串和模式串过长时使用的匹配算法。
朴素模式匹配
朴素模式匹配(Brute-Fore)算法又称为BF算法,算法的思想:
使用子串从主串的第一个字符依次开始匹配。
如果失配,则用主串的下一个字符重新和子串的第一个字符比较,然后一次类推,若到最后仍匹配失败,则返回-1。
例: 在主串 abcd中匹配子串cd1
2
3
4
5
6abcd
cd 失败
abcd
cd 失败
abcd
cd 成功
每次比较失配后,模式串的指针都要回退到第一个字符,重新和主串下一个字符比较。
算法最多会匹配(m-n+1)次,其中m和n分别是主串和子串的长度。
时间复杂度为T(n)=O((m-n+1)*n),共比较了(m-n+1)遍,每遍比较子串长度个字符。
范例1:BF模式匹配。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//super代表主串。Sub代表子串。m代表主串的长度。n代表子串的长度。
int indexOf(char super[],char sub[],int m,int n){
int i=0,j=0,index=-1; //i用来遍历主串,j用来遍历子串。
while(i<m && j<n){ //如果,子串和主串都没有到结尾,则继续匹配。
if(super[i] == sub[j]){ //如果主串的当前字符和子串相同。
i++;j++; //则继续比较下一个字符。
}else{//如果主串的当前字符和子串不相同。
i = i-j+1; //则主串回到本次比较的起点之后的那个位置。
j = 0; //子串回到开头。
}
}
if(j==n){ //如果子串到达了串尾,则证明匹配成功了。
index = i-j; //计算子串在主串中出现的位置。
}
return index; //返回这个位置,如果没找到子串,则返回index的本身值 -1 。
}
KMP模式匹配
KMP算法是模式匹配专用算法,它是在已知模式串的next或nextval数组的基础上执行的,如果不知道它们二者之一,就没法使用KMP算法,因此我们需要先计算它们。
KMP算法由两部分组成。
第一部分,计算模式串的
next或nextval数组(二者选一即可)。
第二部分,利用计算好的模式串的next或nextval数组,进行模式匹配。
问:next和nextval数组是干什么用的?
答:
首先,next和nextval数组它们都是隶属于子串的。
然后,子串中每一个字符都有一个next或nextval数组的元素与之对应,也就是说如果子串长度为6,则该子串的next和nextval数组的长度就是6,如果子串长度为5,则next和nextval数组长度也就是5。
接着,子串中每个字符对应一个next或nextval数组的元素,当子串和主串进行匹配且失配时,子串不再像BF算法那样,直接回到串首了,而是看子串在哪个字符上失配,就找到那个字符对应的next或nextval数组中的元素,然后跳到该元素所指向的位置上去。
说白了next和nextval数组就是在子串失配时,指明子串应前往的位置,这样就大大减少了比较次数,因此说KMP算法比BF算法性能要高。
KMP算法中有next数组和nextval数组之分,他们代表的意义和作用完全一样,完全可以混用。 唯一不同的是,next数组在一些情况下有些缺陷,而nextval是为了弥补这个缺陷而产生的。 至于什么缺陷,一会说。
Next数组计算方法
首先,正如前面所说,子串在哪个字符上失配,就找到那个字符对应的next数组中的元素。
然后,next数组中的元素值是由它前面位置上的字符的next值推导出。即 “abc”中b字符的next值,由a的next值推导出,c的next值由a或b的next值推导出。最后,开始计算:
1、第1个字符的next数组的值固定为0。
2、计算第n(n>1)个字符的next值时,看第n-1个字符是否和第n-1个字符的next值指向位上的字符相等。
如果相等,则第n个字符的next值就是第n-1个字符的next值+1,即next[n]=next[n-1]+1。
如果不相等,则继续向前找,看第n-1个字符是否和next[next[n-1]]指向的字符相等,如果相等则next[n]=next[next[n-1]]+1,然后重复下去。若直到最后next值=0了都没有找个任何一个字符与第n-1个字符相同,则next[n]=1;
范例1:计算串“A=ababaabab”的next数组。
我们假设数组的下标是从1开始计算。
第一步,按照规定第一个a的next值为0,即next[1]=0;。
第二步,计算第二个字符b的next值,由于b的下标为2,所以进行:
判断A[2-1]是否等于A[next[2-1]],由于next[2-1]值为0,所以next[2]=1。
第三步,计算第三个字符a的next值,由于a的下标为3,所以进行:
判断A[3-1]是否等于A[next[3-1]],结果b!=a。
继续判断A[3-1]是否等于A[next[next[3-1]]],后者next值为0,所以next[3]=1。
第四步,计算第四个字符b的next值,由于b的下标为4,所以进行:
判断A[4-1]是否等于A[next[4-1]],结果a==a,所以next[4]=1+1。
第五步,计算第五个字符a的next值,由于a的下标为5,所以进行:
判断A[5-1]是否等于A[next[5-1]],结果b==b,所以next[5]=2+1。
第六步,计算第六个字符a的next值,由于a的下标为6,所以进行:
判断A[6-1]是否等于A[next[6-1]],结果a==a,所以next[6]=3+1。
第七步,计算第七个字符b的next值,由于b的下标为7,所以进行:
判断A[7-1]是否等于A[next[7-1]],后者为A[4],结果a!=b。
继续判断A[7-1]是否等于A[next[next[7-1]]],后者为A[2],结果a!=b。
继续判断A[7-1]是否等于A[next[next[next[7-1]]]],后者为A[1],结果a==a,所以next[7]=next[2]+1。
第八步和第九步,省略。
最终串“ababaabab”的next数组为:
0 1 1 2 3 4 2 3 4
Nextval数组计算方法
首先要知道nextval数组是在next数组的基础上计算出来的,计算过程:
1、第1个字符的nextval数组的值固定为0。
2、计算第n(n>1)个字符的nextval值时,看第n个字符和它的next值指向位上的字符是否相等。
若相等,则第n位字符的nextval[n]=nextval[next[n]]。
若不相等,则第n位字符的nextval[n]=next[n]。
范例2:计算串“A=ababaabab”的nextval数组。
我们假设数组的下标是从1开始计算。
第一步,按照规定第一个a的nextval值为0,即nextval[1]=0;。
第二步,计算第二个字符b的nextval值,由于b的下标为2,所以进行:
判断A[2]是否等于A[next[2]],结果b!=a,则nextval[2]=1
第三步,计算第三个字符a的nextval值,由于a的下标为3,所以进行:
判断A[3]是否等于A[next[3]],结果a==a,则nextval[3]=0
其它以此类推。
最终串“ababaabab”的nextval数组为:
0 1 0 1 0 4 1 0 1
匹配的过程
得到了模式串的next数组后,就可以开始进行匹配了。
假设主串是“
aab1234”,模式串为“aac”,通过计算模式串的next数组为012。
1、依次比较主串和子串的每一字符,当比较到第三字符c的时候,失配了。
2、此时会将模式串的指针调整到next[3]的值所指向的位置(也就是2),对应的字符是a。
3、接着用a继续和主串中的b比较,显然不相等。
4、接着会将模式串的指针调整到next[2]的值所指向的位置(也就是1),对应的字符是a。
5、接着用a继续和主串中的b比较,显然不相等。
6、接着会将模式串的指针调整到next[1]的值所指向的位置(也就是0),此时已经到头了,说明主串的前三个字符无法匹配子串了,于是将主串的位置后移一位。
将上面的匹配过程带入到nextval数组的话,匹配的次数会比next要少,因而我们实际开发中使用最多的就是nextval数组。
实际开发中,使用C++和Java等语言的人占大多数,它们的下标都是从0开始的,而上面计算next数组时下标都是从1开始的。其实我们规定第一个字符的next值为0,不是完全不能改变的,只要不影响计算结果,第一位的next值也可以不是0。
也就是说,我们可以将下标和next值都-1,即元素的下标的取值从0开始,第一位字符的next数组的值相应的改为-1即next[0]=-1;
范例3:Java版KMP模式匹配。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37public class KMPString {
private int[] getNextVal(String str){
int i=0,j=-1,strLen=str.length();
int[] nextval=new int[strLen];
char[] strArr=str.toCharArray();
nextval[i]=j;
while(i<strLen){
if(j==-1 || strArr[i]==strArr[nextval[j]]){
i++; j++;
if(i<strLen){
if(strArr[i]!=strArr[j])
nextval[i]=j;
else
nextval[i]=nextval[j];
}
}
else
j=nextval[j];
}
return nextval;
}
public int indexOf(String sup,String sub){
int i=0,supLen=sup.length();
int j=0,subLen=sub.length();
int[] nextval=getNextVal(sub);
while(i<supLen && j<subLen){
if(j==-1 || sup.charAt(i)==sub.charAt(j)){
i++; j++;
}
else
j=nextval[j];
}
if(j==subLen)
return i-j;
return -1;
}
}
语句解释:
- i代表当前字符的前一个字符的位置,j最初代表第i个字符的的nextval值。
- 因为有i++操作,因此又判断了一次i,以防止数组越界。
树形结构
树形结构指的是数据元素之间存在着“一对多”的树形关系的数据结构,是一类重要的非线性数据结构。树是由n个结点构成的有限集(n>=0)。
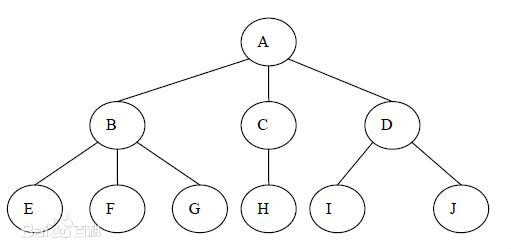
上图就是一个树形结构,A被称为根节点,其它所有节点被称为非根节点。
非根节点有一个父根节点和0个或多个子节点。
B、C、D都有各自的子节点,它们与各自的子节点构成了A节点的子树。
二叉树
二叉树是是一种特殊的树,根节点下只有两个子树,左右子树互不相交。
树高为k的二叉树,最多有2k-1个结点(k>=1)。
二叉树主要采用链式存储.
二叉树最常见的操作就是遍历,遍历分为先序遍历、中序遍历、后序遍历、层次遍历。
范例1:遍历。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23void first(BinaryTree *root){ //本函数用来先序遍历二叉树。
if(root != NULL){ //如果当前结点不为空 则开始遍历。
printf("%d",root->data); //先输出当前结点的数据域。
first(root->left); //遍历其左孩子结点。
first(root->right); //遍历其右孩子结点。
}
}
void middle(BinaryTree *root){ //本函数用来中序遍历二叉树。
if(root != NULL){ //如果当前结点不为空 则开始遍历。
middle(root->left); //先遍历其左孩子结点。
printf("%d",root->data); //再输出当前结点的数据域。
middle(root->right); //最后遍历其右孩子结点。
}
}
void last(BinaryTree *root){ //本函数用来后序遍历二叉树。
if(root != NULL){ //如果当前结点不为空 则开始遍历。
last(root->left); //先遍历其左孩子结点。
last(root->right); //再遍历其右孩子结点。
printf("%d",root->data); //最后输出当前结点的数据域。
}
}
语句解释:
- 先遍历根结点称为先序遍历,其他的类推。
范例2:Java版层次遍历。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15public class TreeFor {
public void floor(Tree root){
// list就代表一个数组,用来存储结点。
ArrayList<Tree> list = new ArrayList<Tree>();
// 先将根节点存储到数组中的最后一个位置。
// 由于此时数组中一个元素都没有,所以root也是第一个元素。
list.add(root);
while(!list.isEmpty()){
Tree current = list.remove(0); //则取出数组中当前第一个元素。
System.out.println(current.getData());//输出这个元素中的数据。
list.add(current.getLchild());//将这个元素的左孩子放入数组最后。
list.add(current.getRchild());//将这个元素的右孩子放入数组最后。
}
}
}
语句解释:
- 思想“从上到下,从左到右”,利用list的特点实现的。
图状结构
图状结构(Graph),是由“顶点”和“边”所组成的集合,通常⽤G=(V,E)来表⽰,其中V是顶点的集合,E是边的结合,其中顶点之间是多对多关系。
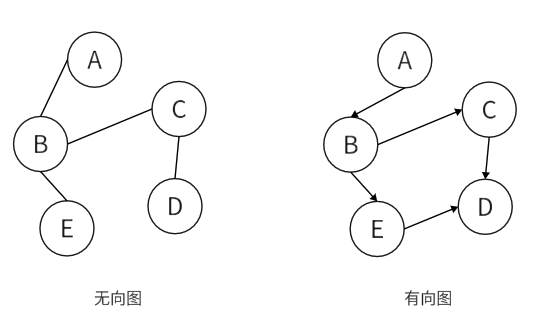
图按照边的方向分为:
无向图:顶点之间没有前后顺序,从A可以到B,从B也可以到A。
有向图:顶点之间有前后顺序,在上方右侧的图中,只能从A到B,不能从B到A。
图的存储结构分为:顺序式和链式,分别使用邻接矩阵和邻接表来表示。
排序
根据排序过程使用的存储器不同分为:
内排序:在内存中进行排序。
外排序:由于待排序数过多内存容不下,因此排序过程中,需要不断地与外存进行数据交换。
衡量排序算法时,从以下三方面观察:
运行时间、关键字比较次数、记录的移动次数。
排序具体的类型有:
插入排序、交换排序、选择排序和一些其它排序。
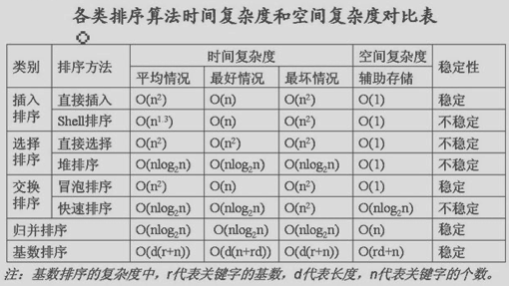
- 最好的情况是: 数据已有序。
- 最坏的情况是: 数据反序存放。
- 平均情况: 随机存放。
插入排序
范例1:直接插入排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14void insertSort(int array[],int n){
int i,j,temp;
for(i=1;i<n;i++){ //从第2个元素开始排序,一直到最后一个元素结束。
temp = array[i]; //将当前元素的值,先存储起来,以方便一会使用。
for(j=i-1;j>=0;j--){ //使用当前元素依次和已排序的元素比较。
if(temp<array[j]){ //如果当前元素比其前面的那个元素小。
array[j+1] = array[j]; //则将该元素后移一个位置。
}else{ //如果当前元素大于或等于其前面的元素。
break; //则不再继续比较。
}
}
array[j+1] = temp; //将当前元素放到指定位置。
}
}
语句解释:
- 直插排序是将第一个数当作成已排好的数,然后不断的拿待排序元素,跟已排好的元素比较:
- 若待插入元素小,则将当前元素后移一位,然后待插入元素继续和再前一位上的元素比较。
- 若待插入元素大于或等于当前元素,则将待插入元素放到当前位置+1处,接着继续排序下一个数。
- 一般来说,如果数据量少时,可以使用此方法排序,如果数据过多,元素后移的次数也就增加了。
范例2:折半插入排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27//本函数用来返回元素应该插入的位置。
int indexOf(int array[],int high,int num){
int low = 0,temp; //从0开始比较,temp用来存放临时位置。
while(low<=high){ //如果位置还没有计算出来,则继续计算。
temp = (low+high)/2; //计算位置。
if(array[temp] <= num){ //如果待插入元素大于temp位置上的元素。
low = temp + 1; //则更新low指针。
}else{
high = temp - 1; //否则更新high指针。
}
}
return high+1; //返回元素应该插入的位置。
}
//本函数用来实现折半插入排序。
void insertSort(int array[],int n){
int i,j,temp,index;
for(i=1;i<n;i++){ //依旧是将第一个元素看作为是已经排好序。
temp = array[i]; //将当前元素保存起来。
//计算出当前元素应该插入的位置。
index = indexOf(array,i-1,array[i]);
//从最后一个元素开始,一直到index之间的元素 后退1位。
for(j=i-1;j>=index;j--){
array[j+1] = array[j];
}
array[j+1] = temp; //将当前元素,插入到数组中。
}
}
语句解释:
- 所谓折半插入排序,即在折半插入排序中,不再使用顺序比较来获得插入位置,而是使用折半查找的方法获取插入位置。
希尔排序
希尔排序算法由两部分组成:分组和排序。
分组:将一个数组进行多次分组,其中第一次分组时,分出的组数最多、每一小组中元素个数最少,最后一次分组时 分出的组数最少、组中元素个数最多。
比如待排序数组中有10个元素:
第一次分组 咱们把它分成5组 每组2个元素。
第二次分组 咱们把它分成2组 每组5个元素。
第三次分组 咱们把它分成1组 每组10个元素。
问:分组之后干什么呢?
分组之后咱们就开始对每一组中的数据进行排序,当所有组都排序完后,再进行下一次分组。
问:那按什么规则分组呢?
比如说数组中十个元素为10 、9、8、7、6、5、4、3、2、1,第一次分组分了5组,每组的内容如下:
第一组:10 和 5
第二组:9 和 4
第三组:8 和 3
第四组:7 和 2
第五组:6 和 1
问:排序的规则是什么?
排完第一组的前2个元素后,就去排第2组的前两个元素,然后如果还有第3组,则就去排第3组的前两个元素,等所有组中的前两个元素都排完后,接着从第一组开始,再对每组第2和第3个元素进行比较排序。
1 | void shell(int array[],int n){ //本函数用来实现希尔插入排序。 |
交换排序
范例1:冒泡排序。1
2
3
4
5
6
7
8
9
10
11
12
13void bubbleSort(int array[],int n){ //本函数用来进行冒泡排序。
int i , j , temp;
// 将数组中最大的元素,不断的放到无序元素中的最后一个位置。
for(i=n-1;i>0;i--){
for(j=0;j<i;j++){ //从第一个元素开始,一次与其后的元素比较。
if(array[j]>array[j+1]){ //如果当前元素大于其后的元素。
temp = array[j]; //则交换元素位置。
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
语句解释:
- 外层循环控制内层循环的终点。
- 内层循环从0开始,依次和相邻元素比较,到i-1结束。
- 总的来说,冒泡排序是依次将最大的元素,放到数组的最后一个位置。
范例2:快速排序。
毫无疑问,快速排序是最流行的排序算法,因为有充足的理由证明,在大多数情况下,快速排序都是最快的(这只对内部排序或随机存储器内而言,而对于外排序来说,其他排序算法可能会更好一些)。快速排序“枢轴”的选择,决定了算法的执行效率,应该避免选择数组中的最大或最小值做枢轴,最好是选择中值,左右两边的长度恰好相等,快速排序是一种不稳定的排序算法。1
2
3
4
5
6
7
8
9
10
11
12
13
14void sort(int[] array,int low,int high){ //本函数用来进行快速排序。
if(low<high){ //如果给出的坐标合法,才可以进行排序。
int pivot=array[low],i=low,j=high; //将第一个元素作为枢轴。
while(i<j){ //如果下标合法。
while(i<j && array[j]>=pivot) j--;//从右端开始不断和pivot比较。
array[i]=array[j]; //将j指向的元素,放到最左边。
while(i<j && array[i]<=pivot) i++; //再从左端开始,不断的比。
array[j]=array[i]; //将j指向的元素,放到最右边。
}
array[i]=pivot; //此时i和j相等,将枢轴放到i的位置中去。
sort(array,low,i-1); //对枢轴左边的元素进行快速排序。
sort(array,i+1,high); //对枢轴右边的元素进行快速排序。
}
}
选择排序
范例1:直接选择排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void sort(int[] array,int n){ //本函数用来进行直接选择排序。
int i,j,k,temp;
for(i=0;i<n-1;i++){//总体思想:不断的将当前数组中最小的元素,放到开头。
k=i; //记录当前元素所在的下标。
for(j=i+1;j<n;j++){ //让当前元素,依次和其后的所有元素比较。
if(array[k]>array[j]){ //如果当前元素大。
k = j; //将另一个参与比较的元素的下标,保存起来。
}
}
if(k != i){ //如果在排序过程中k的值改变了。
int temp=array[k]; //则说明,i所指向的元素并不是最小的。
array[k]=array[i]; //所以,交换i和k指向的元素的位置。
array[i]=temp;
}
}
}
语句解释:
- 总的来说,直接选择排序是不断将数组中最小的元素,放到数组的开头,它与冒泡排序恰巧相对应。
查找
查找分为:静态查找和动态查找。
静态查找:只是纯粹的查找,不修改数据。
动态查找:查找时会修改数据。
查找表:
有n条记录的集合T是实施查找的数据基础,T称为“查找表”(Search Table)。
范例1:顺序查找。1
2
3
4
5
6
7
8
9int indexOf(int array[],int keyword,int n){ //本函数用来进行顺序查找。
int i;
for(i=0;i<n;i++){ //从数组的第一个元素开始匹配,一直到最后一个元素结束。
if(array[i] == keyword){ //如果匹配成功,则返回这个元素的位置。
return i;
}
}
return -1; //如果直到最后,都未匹配成功,则返回-1。
}
范例2:二分查找。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15int indexOf(int[] array,int keyword,int n) {
int low=0,high=n-1,temp;
while(low<=high) {
temp=(low+high)/2;
if(array[temp] == keyword)
return temp;
else if(array[temp]>keyword) {
high = temp-1;
}
else {
low=temp+1;
}
}
return -1;
}
语句解释:
- 二分查找又被称为折半查找,要求数组中的元素必须是有序存放的,否则无法查找成功。
- 折半查找是建立在顺序存储结构之上的,插入和删除不方便。
二叉查找树
二叉查找树(Binary Search Tree) 又称二叉排序树、二叉搜索树、有序二叉树,它就是一棵普通的二叉树。二叉查找树的特点:
若当前结点的左子树非空,则它左子树上的所有结点的值都小于它。
若当前结点的右子树非空,则它右子树上的所有结点的值都大于它。
它的左右子树本身也是一棵二叉查找树。
对二叉查找树进行中序遍历可得到从小到大的排列。
二叉查找树的查找次数不会超过树的深度,其进行查找时的效率与树的形状有关(单支时最坏)。
BST中不能有重复元素。
范例1:C语言版二叉查找树。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
struct Node{ // 定义一个结点结构体。
int data; // 结点的数据域。
struct Node *left; // 结点的左子树。
struct Node *right; // 结点的右子树。
};
typedef struct Node Tree; // 给这个结点结构体起一个别名Tree。
Tree* create(int data){ // 本函数用来建立一个结点。
Tree* node = (Tree *)malloc(sizeof(Tree *)); // 从内存中开辟空间。
node->data = data; // 初始化数据域。
node->left = NULL; // 将新结点的左子树设为NULL。
node->right = NULL; // 将新结点的右子树设为NULL。
return node; // 返回新建立的结点。
}
Tree *insert(Tree *root,int data){ // 本函数用来向BST中插入一个元素。
if(root == NULL){ // 如果当前结点为空,则建立这个结点。
return create(data);
}else{ // 如果当前结点不为空。
if(root->data == data){ // 判断要插入的结点的数据域,是否已经存在。
return NULL; // 如果存在,则不允许插入。
}else if(root->data>data){ // 如果当前结点的data大于参数data的值。
// 则将欲插入结点插入到本结点的左子树。
Tree *temp = insert(root->left,data);
if(temp !=NULL){ // 如果当前结点的左子树本来为空。
root->left = temp; // 则将新结点,放到本结点的左子树中。
}
return NULL; // 接着,再返回NULL。
}else{
// 如果当前结点的data小于参数data的值。
// 将欲插入结点插入到本结点的右子树。
Tree *temp = insert(root->right,data);
if(temp !=NULL){ // 如果当前结点的右子树本来为空。
root->right = temp; // 则将新结点,放到本结点的右子树中。
}
return NULL; // 接着,再返回NULL。
}
}
}
void print(Tree *root){ // 本函数用来中序遍历一个二叉树。
if(root != NULL){ // 如果根节点不为NULL 则继续遍历。
print(root->left); // 先递归遍历其左子树。
printf("%d ",root->data); // 然后输出当前结点的data域。
print(root->right); // 最后再变量当前结点的右子树。
}
}
main(){ // 本函数用来测试BST。
Tree *root = NULL; // 首先建立一个根节点指针。
root = insert(root,5); // 将根节点插入到BST中。
insert(root,3); // 再插入3到BST中。
insert(root,4); // 再插入4到BST中。
print(root); // 中序遍历BST。
putchar('\n'); // 换行。
}
Tree *search(Tree *root,int data){ // 本函数用来从BST中查找一个元素。
if(root == NULL){ // 如果一直到最后都没有找到,则返回NULL。
return NULL;
}else{ // 若当前根结点不等于NULL。
if(root->data == data){ // 则判断当前节点的data域是否和参数data相等。
return root; // 如果相等,则代表找到了这个结点。
}else if(root->data>data){ // 如果当前结点的data域大,则去其左子树找。
return search(root->left,data);
}else{// 如果当前结点的data域小,则去其右子树中找,并返回其查找结果。
return search(root->right,data);
}
}
}
BST删除元素时有三种情况:
待删结点无孩子结点,此时直接删掉这个结点即可。
待删节点只有左孩子或只有右孩子,此时将此结点的左孩子或者右孩子上移即可。
待删节点左右孩子都存在,此时可以这么处理:用左子树根结点或右子树根节点取代待删节点,若使用左子树替代,且左子树本身还也有右子树,则左子树的右子树,放到待删结点右子树的最左端。反过来如果用右子树顶替,且右子树本身也有左子树,则将右子树的左子树放到待删结点左子树的最右端。
散列查找
顺序、折半、索引表、二叉查找树的查找效率都与查找表的长度紧密相关,需要使用关键字不断的和查找表中的元素进行匹配。而查找的理想做法是不去或很少进行匹配,散列查找就是通过散列函数来计算元素的位置,从而尽可能的减少匹配次数。
在散列查找中使用的函数称为“散列函数”或哈希函数。
在散列查找中的查找表称为散列表或哈希表。
如果两个不同的关键字的散列函数值相同,则这种现象就称为“冲突”,这两个关键字被称为“同义词”,由“同义词”产生的冲突称为同义词冲突。
冲突处理,即使计算的再准确,散列函数值也难免会有冲突出现,常用的冲突处理的方法:
开放定址法:采用开放定址法时,散列表被存储在一个一维数组中,把散列表里的可用位置向处理冲突开放。
线性探索:如果当前位置起了冲突,则走向下一个位置,如果走到最后,则从0开始重走,如果散列表已满,则停止。
二次探索:如果当前位置起了冲突,则依次使当前下标加上一个位移量,然后再重新尝试插入,位移量为:(12,-12, 22,-22,… ,k2,-k2) 其中k<=m/2 m为散列表的长度。
随机探测:如果当前位置起了冲突,使当前下标+一个数随机出来的数。
链地址法 :将同义词用单链表接在一起,组成同义词链表。如图: